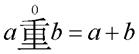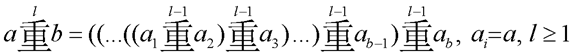M. Vincent van Mechelen, 80.14.1

CHONG AND/OR HYPER?
Particular Questions in Arithmetic Universalization

[maximum design width 9*64=576 pixels]

The Basic Formulas of the Chong Operators


Chong symbol, with expression in words (and in informal handwriting)
重(a,l,b) ≡ chong(a,l,b) ≡ 工(a,l,b)
 The use of 重 as a function in a 'one-dimensional' representation

Definition of the chong operator on the (plus-)zero level

Definition of the chong operator on the l-th level of iteration

Definition for inverse chong operators

Equations for the 1st and the 2nd level of iteration
Origin: Chinese 重, zhòng or chóng; chóng means again, repeat


The Formulas of Hyperoperations

Hn(a,b) = Hn-1(a,Hn(a,b-1)), n>0, b>0
H0(a,b)=b+1; H1(a,0)=a;
H2(a,0)=0; Hn(a,0)=1, n≥3
The defining formulas in line with Goodstein, who coined the terms tetration and pentation
For n≥4, Hn(a,b) is in words a n-ated to b

Thus, H4(a,b) is "a 'tetrated' to b"
H1(a,b)=a+b; H2(a,b)=a*b; H3(a,b)=a↑b

Equations for the 1st, 2nd and 3rd levels
Hn(a,b) = a↑n-2b, n>2, a≥0, b≥0

Equation for the 3rd and following levels
hn(a,b) = hn-1(hn(a,b-1),a)
A formula for 'lower-hyperoperations'
Origin: Greek ὑπέρ, hupér, meaning over or above; the antonym of hyper is hypo, meaning under



Three zero levels in two arithmetic universalizations
Chong levels Hyper level 0
Positive +0 Negative -0
the first of an infinite num­ber of positive levels:
the level of (noniterative) addition		 the first of an infinite num­ber of negative levels:
the level of (noniterative) subtraction		 the first of an infinite num­ber of (non­negative) levels:
a level of incrementation
重(a,+0,b)=a+b 重(a,-0,b)=a-b H0(a,b)=b+1
重(a,+0,1)=a+1
重(b,+0,1)=b+1		 重(a,-0,1)=a-1
重(b,-0,1)=b-1
successor operation,
unrepeated increment,
an instance of addition		 predecessor operation,
unrepeated decrement,
an instance of subtraction		 successor operation,
increment(ation),
zeration
positive numbers are de­fined by 重(0,+0,1)=+1,
重(+1,+0,1)=+2,
重(+2,+0,1)=+3, et cetera; each step is an increment		 negative numbers are de­fined by 重(0,-0,1)=-1,
重(-1,-0,1)=-2,
重(-2,-0,1)=-3, et cetera; each step is a decrement		 an increment is defined by 1+1+1+...+1[b copies] +1 = b+1
重(重( ... 重⁠(0,+0,1) ... ,+0,1),+0,1) =
1+1+ ... +1=b 		重(重( ... (重⁠(0,-0,1) ... ,-0,1),-0,1) =
-1-1- ... -1=-b		 1+1+1+...+1[b copies]
重(重(b,+1,+1),+0,1) = b+1 重(重(b,+1,-1),-0,1) = -b-1 b+1
iterative incrementation,
an addition on top of a positive multiplication		 iterative decrementation,
a subtraction on top of a negative multiplication
Differences or changes on the zero level have no repercussions on successive or preceding levels, except for their numbering.


Left-associative versus right-associative evaluations
No such distinction if only two operands: 2^2=4, 2^3=8, 3^2=9, 3^3=27
Exponentiation, Evaluation
three operands left-associative right-associative
2^2^2 (2^2)^2=4^2=16 2^(2^2)=2^4=16
2^2^3 (2^2)^3=4^3=64 2^(2^3)=2^8=256
2^3^2 (2^3)^2=8^2=64 2^(3^2)=2^9=512
2^3^3 (2^3)^3=8^3=512 2^(3^3)=2^27=134,217,728
3^3^3 (3^3)^3=27^3=19,683 3^(3^3)=3^27=7,625,597,484,987


Correspondences at the first seven nonnegative chong levels
Left-associative Right-associative
chong operator hyperoperation Knuth notation
Chong +0 Addition (+), Hyper-1 None
Chong +1 Multiplication (x or *), Hyper-2 None
Chong +2 Exponentiation (^ or **), Hyper-3 One up-arrow (↑)
Chong +3 (Re)iterative exponentiation
Tetration, Hyper-4		 Two up-arrows (↑↑)
Chong +4 Twofold (re)iterative exponentiation
Pentation, Hyper-5		 Three up-arrows (↑↑↑)
Chong +5 Threefold (re)iterative exponentiation
Hexation, Hyper-6		 Four up-arrows (↑↑↑↑)
Chong +6 Fourfold (re)iterative exponentiation
Heptation, Hyper-7		 Five up-arrows (↑↑↑↑↑)


JavaScript Functions for Hyper and Chong Calculations

 function knuth(a, k, b) {
  if (b === 0) {
    return 1;
  }
  if (k === 1) {
    return a ** b;
  }
  return knuth(a, k - 1, knuth(a, k, b - 1)); 
 }

On the internet the above function may be called "knuth_arrow" or "knuthArrows". See, for example, www.dcode.fr/knuth-arrows, www.geeksforgeeks.org/knuths-up-arrow-notation-for-exponentiation/ and (for a pseudocode) googology.fandom.com/wiki/Hyper_operator 

 function chong(a,l,b)  // l is order number of chong level
 {
  if (l===0) return a+b;  // zero level defined traditionally 
   else
    {
     if (l===1) return a*b;  // 1st level traditionally
      else
       {
        if (l===2) return a**b;  // 2nd level traditionally
         else
          {
           if (b===1) return a;  // iteration b times only
           return chong(chong(a,l,b-1),l-1,a);   // for l>2,
             // defined recursively the left-associative way
          }
       }
    }
 }

This code (with explanations) for the chong function was written by the author MVvM, 80 aSWW.


CHONG LEVEL PLUS-0 & HYPER LEVEL 1: ADDITION

Chong-0 and Hyper-1 core results for chong(a,+0,b)≤10
a, b 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10
4 5 6 8 9 10
5 6 7 9 10
6 7 8 10
7 8 9
8 9 10
28 core results in total:
16 in the inner core,
2*6 in the outer core
9 10
Chong-0 results between 2 and 10 (and beyond to infinity):
generable: 4, 5, 6, 7, 8, 9, 10 (11, 12, 13, 14, 15, 16, 17, 18 etc.)
nongenerable: 2 and 3 (outside the core where a≥2 and b≥2)

CHONG LEVEL PLUS-1 & HYPER LEVEL 2: MULTIPLICATION

Chong-1 and Hyper-2 core results for chong(a,+1,b)≤25
a, b 1 2 3 4 5 6 7 8 9 10 11 12 13
1 1 2 3 4 5 6 7 8 9 10 11 12 13
2 2 4 6 8 10 12 14 16 18 20 22 24
3 3 6 9 12 15 18 21 24
4 4 8 16 20 24
5 5 10 20 25
6 6 12 24
7 7 14
8 8 16
9 9 18
10 10 20
11 11 22
38 core results:
16 in the inner core,
2*11 in the outer core
12 12 24
13 13
Connections with chong-0 core results:
chong(2,1,2) = 重(2,0,2)=4;
chong(2,1,3) = 重(重(2,0,2),0,2) = 重(4,0,2)=6;
chong(2,1,4) = 重(重(重(2,0,2),0,2),0,2) =
重(重(4,0,2),0,2) = 重(6,0,2)=8;
chong(2,1,5) = 重(重(重(重(2,0,2),0,2),0,2),0,2) =
重(重(重(4,0,2),0,2),0,2) = 重(重(6,0,2),0,2) =
重(8,0,2)=10;
chong(3,1,2) = 重(3,0,3)=6;
chong(4,1,2) = 重(4,0,4)=8;
chong(5,1,2) = 重(5,0,5)=10
Chong-1 results between 2 and 25 (and beyond to infinity):
generable: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25 (etc.)
nongenerable: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 etc.
(these non-results are traditionally called "prime numbers")

CHONG LEVEL PLUS-2 & HYPER LEVEL 3: EXPONENTIATION

Chong-2 and Hyper-3 core results for chong(a,+2,b)≤3125
Organic table with chong(a,2,b) = knuth(a,1,b)
a, b 1 2 3 4 5 6 7 8 9 10 11 12
1 1 1 1 1 1 1 1 1 1 1 1 1
2 2 4 8 16 32 64 128 256 518 1036 2072
3 3 9 27 81 243 729 2187
4 4 16 256 1024
5 5 25 625 3125
6 6 36 1296
7 7 49 2401
8 8 64
9 9 81 729
10 10 100 1000
11 11 121 1331
12 12 144 1728
85 core results in total:
16 in the top-left core,
8 in the top-right core,
61 in the bottom-left core
13 13 169 2197
14 14 196 2744
15 15 225
16
-
54		 16
-
54		 256 | 289 | 324 | 361 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 | 2500 | 2601 | 2704 | 2809 | 2916
55 55 3025
56 56
Connections with chong-1 core results:
chong(2,2,2) = 重(2,1,2)=4;
chong(2,2,3) = 重(重(2,1,2),1,2) = 重(4,1,2)=8;
chong(2,2,4) = 重(重(重(2,1,2),1,2),1,2) =
重(重(4,1,2),1,2) = 重(8,1,2)=16;
chong(3,2,2) = 重(3,1,3)=9;
chong(4,2,2) = 重(4,1,4)=16;
chong(5,2,2) = 重(5,1,5)=25
Chong-2 results between 2 and 3125 (and beyond to infinity):
generable: 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 128,
144, 169, 121, 225, 256, 289, 324, 361 etc. (see table above)
nongenerable: 2, 3, 5, 6, 7, 10, 11, 12, 13, 14, 15, 17, 18, 19 etc.

CHONG LEVEL PLUS-3 & HYPER LEVEL 4:
REITERATIVE EXPONENTIATION

Chong-3 table with all chong(a,+3,b) core results
The 29 results in the 3rd to 10th columns are typical of the chong operator
a, b 1 2 3 4 5 6 7 8-10 11
1 1 1 1 1 1 1 1 1 | 1 | 1 1
2 42949\
67296		 1.8\
e19		 3.4e38 |
1.2e77 |
1.3e154		 In-
fin-
ity
chong(2,3,2): all values in column 2 of the Chong-3 table are exactly the same as those in column 2 of the Hyper-4 table;
, which should be 18446744073709551616; ;
the horizontal sequence at a=2 from b=2, which does not occur in the Hyper-4 table, is the (first) sequence of squares of squares, which plays a pivotal role in a universal integrated linguistic-mathematical numeral system
3 762559\
7484987		 4.4e38 8.7e115 In-
fin.
as calculated by JavaScript in the source code, or (((3^3)^3)^3)^3 = 4.4342648824303776994824963061915e+38 with a scientific calculator;
4 42949\
67296		 3.4e38 1.3e154 Infin-
ity
chong(4,3,4)= or, with a calculator, ((4^4)^4)^4 = 340282366920938463463374607431768211456;
or, with a calculator, (((4^4)^4)^4)^4 = 1.3407807929942597099574024998206e+154
5 298023\
223876\
953125		 2.4e87
chong(5,3,3) should be (5^5)^5 = 298,023,223,876,953,125, but the JavaScript calculation yields with a final digit which is not even possible;
or, with a calculator, ((5^5)^5)^5 = 2.3509887016445750159374730744445e+87
chong(5,3,5)=Infinity provisionally on the basis of a JavaScript calculation in the source code of this page. It is very well possible, however, to calculate (((5^5)^5)^5)^5 = 7.18212087483073508066162477348e+436 by means of a scientific calculator. Robert Munafo speaks of a (left-associative) "lower hyper4 operator" and offers a table which extends up to a=6 and b=6, with the largest result being 8.019051e+6050.
See https://www.mrob.com/pub/math/hyper4.html.
6 1.0e28 1.2e168
or (6^6)^6 = 10,314,424,798,490,535,546,171,949,056 with a scientific calculator;
or ((6^6)^6)^6 = 1.2041208676482351082020900568573e+168
7 2.6e41 7.4e289
or (7^7)^7 = 2.5692357752105887808861147722424e+41 with a calculator;
8 1677\
7216		 6.3e57
9 3874\
20489		 2.0e77
10 10000\
000000
or 'one googol'
11 285311\
670611		 1.0e126
12 891610\
0448256		 2.5e155
13 3028751\
06592253		 1.8e188
14 111120\
068255\
58016		 4.4e224
15 437893\
890380\
859375		 4.2e264
chong(15,3,2)=15^15, of which the calculated value is shown in the cell above instead of , which is an incorrect notation for a 'rounded-off' number with an im­pos­si­ble final digit (5 being the only one possible);
the same applies to the two numbers in the second column in the following two rows: chong(16,3,2)=16^16 as shown in the cell below instead of , also with an im­pos­si­ble final digit (other than 6); and chong(17,3,2)=17^17 (with 9, 3, 1 and 7 as alternating final digits), not , which is, even if rounded off in the correct way, still more inaccurate;
16 1844674\
4073709\
551616
171 core results in total:
15 in the top-left core,
6 in the top-right core,
150 in the bottom-left core
(138 in col. 2, 12 in col. 3 & 4)
17 8272402\
6188633\
6764177
18
-
79		 18
-
79		 3.9e22 | 2.0e24 | 1.0e26 | 5.8e27 | 3.4e29 | 2.1e31 | 1.3e33 | 8.9e34 | 6.2e36 | 4.4e38 | 3.3e40 | 2.6e42 | 2.1e44 | 1.7e46 | 1.5e48 | 1.3e50 | 1.2e52 | 1.1e54 | 1.1e56 | 1.1e58 | 1.1e60 | 1.1e62 | 1.2e64 | 1.3e66 | 1.5e68 | 1.7e70 | 2.1e72 | 2.5e74 | 3.1e76 | 3.9e78 | 5.0e80 | 6.6e82 | 8.9e84 | 1.2e87 | 1.7e89 | 2.4e91 | 3.5e93 | 5.2e95 | 7.9e97 | 1.2e100 | 1.9e102 | 3.0e104 | 4.9e106 | 8.0e108 | 1.3e111 | 2.3e113 | 3.9e115 | 6.9e117 | 1.2e120 | 2.2e122 | 4.1e124 | 7.6e126 | 1.4e129 | 2.8e131 | 5.3e133 | 1.1e136 | 2.1e138 | 4.3e140 | 8.7e142 | 1.8e145 | 3.8e147 | 8.2e149
80 1.8e152 Infinity
81
-
142		 81
-
142		 3.9e154 | 8.6e156 | 1.9e159 | 4.4e161 | 1.0e164 | 2.3e166 | 5.5e168 | 1.3e171 | 3.1e173 | 7.6e175 | 1.9e178 | 4.7e180 | 1.2e183 | 3.0e185 | 7.7e187 | 2.0e190 | 5.2e192 | 1.4e195 | 3.7e197 | 1.0e200 | 2.7e202 | 7.5e204 | 2.1e207 | 5.9e209 | 1.7e212 | 4.8e214 | 1.4e217 | 4.1e219 | 1.2e222 | 3.6e224 | 1.1e227 | 3.3e229 | 9.9e231 | 3.1e234 | 9.6e236 | 3.0e239 | 9.5e241 | 3.0e244 | 9.8e246 | 3.2e249 | 1.0e252 | 3.4e254 | 1.1e257 | 3.8e259 | 1.3e262 | 4.4e264 | 1.5e267 | 5.3e269 | 1.8e272 | 6.5e274 | 2.3e277 | 8.2e279 | 3.0e282 | 1.1e285 | 3.9e287 | 1.4e290 | 5.4e292 | 2.0e295 | 7.6e297 | 2.9e300 | 1.1e303 | 4.2e305
143 1.6e308 Infinity
chong(143,3,2) =
144
The provisional practical value of chong(144,3,2) = on the basis of a JavaScript calculation in the source code of this page. However, it can be established that 144^144 = 6.3708717381247861841182616291357e+310 with a scientific calculator.
[HIDE DETAILS]
Connections with chong-2 core results:
chong(2,3,2) = 重(2,2,2)=4;
chong(2,3,3) = 重(重(2,2,2),2,2) = 重(4,2,2)=16;
chong(2,3,4) = 重(重(重(2,2,2),2,2),2,2) =
重(重(4,2,2),2,2) = 重(16,2,2)=256;
chong(3,3,2) = 重(3,2,3)=27;
chong(4,3,2) = 重(4,2,4)=256;
chong(5,3,2) = 重(5,2,5)=3125
Hyper-4 table with all knuth(a,2,b) core results
a, b 1 2 3 4 5
1 1 1 1 1 1
2 2 Infinity
knuth(2,2,5)=Infinity provisionally, but the result will be 2↑↑5=2.00352993e+19728 with the calculator at https://www.dcode.fr/[ ]knuth-arrows
3 3 762559\
7484987		 Infinity Infinity
knuth(3,2,4)=Infinity provisionally. Robert Munafo shows a table which extends up to a=6 and b=6, with this number being the largest 'flat' result, that is, with only one exponent of 10 and no other exponents: 3↑↑4 = 1.26×10^3638334640024 = 1.26e+3638334640024. See https://www.mrob.com/[ ]pub/math/hyper4.html
4 4 1.3e154 Infinity Infinity
knuth(4,2,3)=
5 5 Infinity Infinity Infinity
knuth(5,2,3)=Infinity provisionally, but the result will be 5↑↑3 = 1.91101260e+2184 with the calculator at https://www.dcode.fr/[ ]knuth-arrows
6 6 Infinity
7 7 Infinity
8 8 16777216
9 9 387420489
10 10 10000000000
11 11 285311670611
146 core re­sults in total:
8 in the top-left core,
138 in the bot­tom-left core
12 12 891610\
0448256
13 13 3028751\
06592253
14 14 11112006\
825558016
15 15 437893890\
380859400
16
-
142		 16
-
142		 All core results in the sec­ond column of the Hyper-4 table equal those in the same col­umn of the Chong-3 table above.
143 1.6e308 Infinity
knuth(143,2,2) =
144
[HIDE DETAILS]
Connections with hyper-3 core results:
knuth(2,2,2) = knuth(2,1,2)=4;
knuth(2,2,3) = knuth(2,1,knuth(2,1,2)) = knuth(2,1,4)=16;
knuth(3,2,2) = knuth(3,1,3)=27;
knuth(4,2,2) = knuth(4,1,4)=256;
knuth(5,2,2) = knuth(5,1,5)=3125

Chong-3 results between 2 and 1.3e+154, and beyond to infinity:
generable: at least 4, 16, 27, 256, 3125, 19683, 65536, 4294967296, 7625597484987, 298023223876953150 and four more numbers close to 3.4e+38, 4.4e+38, 2.4e+87 and 1.3e+154;
nongenerable: 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21, 22, 23 etc.

CHONG LEVEL PLUS-4 & HYPER LEVEL 5:
TWOFOLD REITERATIVE EXPONENTIATION

Chong-4, 4 chong(a,+4,b) core results
a, b 1 2 3 4
1 1 1 1 1
2 2 4 256 Inf.
chong(2,4,4)=Infinity provisionally, but the result will be 256^256=3.23170061e+616 with the calculator at dcode.fr/[ ]exponentiation-calculation.
3 3 Infin. Inf.
chong(3,4,3)=Infinity provisionally and 19683^387420489 gives a number with more than 10000 digits;
chong(3,4,4)=Infinity provisionally and 19683^(19683^774840980) gives a number with even more digits
4 4 3.40282e+38 Infin. Inf.

chong(4,4,3)=Infinity provisionally and 4^(4^195) gives a number with more than 10000 digits;
chong(4,4,4)=Infinity provisionally and 4^(4^(3*(4^195)+195)) gives a number with even more digits
5 5 Infinity Infin. Inf.
chong(5,4,2) = chong(5,3,5) = Infinity provisionally, but 7.18212087483073508066162477348e+436 by means of a calculator (see chong-3 table above)
[HIDE DETAILS]
Connections with chong-3 core results:
chong(2,4,2) = 重(2,3,2)=4;
chong(2,4,3) = 重(重(2,3,2),3,2) = 重(4,3,2)=256; 
chong(3,4,2) = 重(3,3,3)=19683;
chong(4,4,2) = 重(4,3,4) = 3.402823669209385e+38
Hyper-5, 3 knuth(a,3,b) core results
a, b 1 2 3 4
1 1 1 1 1
2 2 4 65536 Err.
knuth(2,3,4) too large for memory; 2↑↑↑4 = 2↑↑(2↑↑(2↑↑2)), 2↑↑2=4, 2↑↑4=65536; 2↑↑65536 gives a number with more than 10^1000 digits
3 3 7625597484987 Error Err.
knuth(3,3,3) too large for memory; 3↑↑↑3 = 3↑↑(3↑↑3), 3↑↑3=7625597484987; 3↑↑7625597484987 invalid, because maximum b=1000000
4 4 Infinity Error Err.
knuth(4,3,2)=Infinity provisionally and 4↑↑↑2 = 4↑↑4 = 4^(4^(4^4)), 4^4=256, 4^256 = 1.3407807929942597099574024998206e+154; 4^1.34078079e+154=Invalid input
5 5 Error Err.
[HIDE DETAILS]
Connections with hyper-4 core results:
knuth(2,3,2) = knuth(2,2,2)=4;
knuth(2,3,3) = knuth(2,2,knuth(2,2,2)) =
knuth(2,2,4) = 65536;
knuth(3,3,2) = knuth(3,2,3) = 7625597484987

Chong-4 results between 2 and 7.2e+436:
generable: 4, 256, 19683 and one number close to 3.4e+38
nongenerable: 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21, 22 etc.

Error message: "Uncaught RangeError: Maximum call stack size exceeded"

CHONG LEVEL PLUS-5 & HYPER LEVEL 6:
THREEFOLD REITERATIVE EXPONENTIATION

Chong-5, 2 chong(a,+5,b) core results
a, b 1 2 3 4
1 1 1 1 1
2 2 3.402824e+38 Err/Inf?
3 3 Inf. Err./Infinity? Error
4 4 Inf. Error Error
[HIDE DETAILS]
Connections with chong-4 core results:
chong(2,5,2) = 重(2,4,2)=4;
chong(2,5,3) = 重(重(2,4,2),4,2) = 重(4,4,2) =
3.402823669209385e+38
Hyper-6, 1 knuth(a,4,b) core result
a, b 1 2 3 4
1 1 1 1 1
2 2 4 Error Error
3 3 Error Error Error
4 4 Error Error Error
[NO MORE DETAILS]
Connection with hyper-5 core result:
knuth(2,4,2) = knuth(2,3,2)=4

Chong-5 results between 2 and the smaller of chong(2,5,4) and chong(3,5,2):
generable: 4 and one number close to 3.402823669209385e+38
nongenerable: 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21, 22 etc.

Error message: "Uncaught RangeError: Maximum call stack size exceeded"

CHONG LEVEL PLUS-6 & HYPER LEVEL 7:
FOURFOLD REITERATIVE EXPONENTIATION

Chong-6, 1 chong(a,+6,b) core result
a, b 1 2 3 4
1 1 1 1 1
2 Error
3 Error Error Error
4 Error Error Error
Connection with chong-5 core result:
chong(2,6,2) = 重(2,5,2)=4
Hyper-7, 1 knuth(a,5,b) core result
a, b 1 2 3 4
1 1 1 1 1
2 Error Error
3 Error Error Error
4 Error Error Error
Connection with hyper-6 core result:
knuth(2,5,2) = knuth(2,4,2)=4

Chong-6 results between 2 and the smaller of chong(2,6,3) and chong(3,6,2):
generable: 4 (the only core result obtainable by current JavaScript code);
nongenerable: 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 etc.

Error message: "Uncaught RangeError: Maximum call stack size exceeded"


SEVEN CHONG AND HYPER LEVELS COMPARED

Core results for chong(a,l,b) and knuth(a,l+1,b)
l range considered typical
chong		 com­mon typical
hyper
+0 重(a,+0,b)≤10 none 281 none
+1 重(a,+0,b)≤25 none 38 none
+2 重(a,+0,b)≤3125 none 85 none
+3 all up to 'Infinity'2 33 (19.3%)3 138 8 (5.4%)
+4 all up to 'Infinity' 3 (75.0%) 1 2 (66.7%)
+5 all up to 'Infinity' 1 (50.0%) 1 none
+6 all up to 'Infinity' none 1 none
Totals for these levels: 37 (16.2%) 292 10 (3.3%)
1 The figures in this column show the number of results which are common to the chong and hyper methods.
2 Infinity is the result given when the calculated value ex­ceeds a num­ber close to, but smaller than, 144^144  = 6.4e+310, which is 6.4e+210*1.0e+100 or 6.4*10^210 times 'one googol'.
3 The percentages are based on the method-specific totals of the lev­el(s) concerned, such as 171 and 146 for l=+3.