SUMMARY
Addition, multiplication and exponentiation with their inverses are merely the
lower-level operations of a universal system which has never received any
due attention before.
In this paper
i* will do the least someone
can do who cannot digest the idea that it is completely arbitrary for
contemporary mathematics to keep on stopping reiterating after exponentiation,
that is, so long as no-one has taken the trouble to prove that this
traditional self-limitation is not arbitrary.
I will show what a universal system of arithmetic operations based on their
level of reiteration can or will look like.
INTRODUCTION
From an early age people are being spoon-fed with the four so-called
'fundamental' operations of arithmetic and, perhaps, also the notion of
multiplication as a form of repeated addition and raising a number to a
power as a form of repeated multiplication.
But the spoon they are fed with has limited dimensions.
They are not told what universal system these operations are part
of (in which case fundamental means no more than
lower-level) or why the mathematical operations on higher levels
of reiteration than multiplication and exponentiation would not be interesting,
let alone matter.
Perhaps, the numbers are 'getting too large' with reiterative exponentiation,
but numbers are never small or large in any absolute sense, even not when
an inadequate notational system (with exponentiation on the highest level)
cannot cope with them anymore.
Moreover, with each operation on a higher level, its inverse will follow,
and these inverses on the higher levels of reiteration will, one would
expect, only make the numbers 'proportionately' smaller!
Twenty-six years before the publication of the present article the
was published on paper.
The first book of this Model,
,
contains a section about
with the following last four (slightly abridged) paragraphs:
As the kinds of
derivations are closely related to the kinds of mathematical operation, it
is worth our while to briefly consider the position of the simplest
mathematical operations.
The first pair of operations is, then, that of addition ... and
subtraction ... .
There is no repetition involved in these operations.
In the theory of catenas it is the derivation of a comparative and
equidimensional catena which is the analog of the mathematical sort of
operation on this zero level of reiteration.
...
The prototypical mathematical operation on the first level of
reiteration is multiplication ... .
This is in the first instance nothing else than a form of reiterative
adding-up ... .
Its correlative is division ... .
The derivations of nonequidimensional differential and integral catenas,
and of quotient and product catenas, are the catenical analogs of
mathematical operations on this level.
The prototypical mathematical operation on the second level of
reiteration is exponentiation or the raising of a quantity to power ... .
This is in the first instance nothing else than a form of reiterative
multiplication ...
The correlative of this second-level operation is evolution, the
extraction of a mathematical root ... .
In their original shape the numbers were what mathematicians
traditionally call "natural".
It would be naive to take it for granted now that the number of sorts of
mathematical operation is thus exhausted.
For we can continue ad infinitum by repeating the operation on the
previous level of reiteration.
On the third level this would involve reiterative exponentiation with its
related forms of operation.
But on this and higher levels ordinary, and also mathematical, language
just lack the terminology to express ourselves, even if we would like to.
Nevertheless, it is possible to develop a universal notational system for
reiterative operations of all levels by means of novel mathematical
symbols.
...
Whether we will ultimately need more than one new symbol in mathematics and
more than one new word or even morpheme in This Language remains to be seen.
But we will need at least one.
Entirely in line with the aversion shown in the Model to all forms of
racial, ethnic and territorial exclusivism, i will not turn automatically
to the classical and contemporary languages of traditional mathematics.
For the universalization of arithmetic i will be so bold as to deviate from
the use of the symbols of Mediterranean origin and introduce the East-Asian
symbol 重.
Pronounced "chong" in Putonghua Chinese this character means
to repeat or repetition.
It could not be more appropriate.
ADDITION, MULTIPLICATION AND EXPONENTIATION
An addition such as a+b=c, in which
b≠a, does not involve any form of repetition or
(re)iteration.
(I may be using the prefix re- where it is indeed an iteration
which is being iterated, that is, on a higher level.)
Even in a+b=c with b=a, and therefore
c=a+a, the repetition is not systematic but purely
coincidental.
The repetition does not become systematic until it is part of a system
in which ((...((a+a)+a)+...+a)+a)+a=c
or
((...((a1+a2)+a3)+ ...
+ab-2)+ab-1)+ab=c,
where ai=a.
It is not until then that we multiply a by b, a
multiplication which amounts to repeated addition:
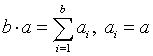
Again, a multiplication such as b·a=c or
a·b=c, in which b≠a, does not
involve any form of repetition apart from the systematic repetition
inherent in the operator itself.
Even in a·b=c with b=a, and
therefore c=a·a, the repetition is not
systematic but purely coincidental.
The repetition does not become systematic until it is part of a system
in which ((...((a·a)·a)· ...
·a)·a)·a=c
or
((...((a1·a2)·a3)·
...
·ab-2)·ab-1)·ab=c,
where ai=a.
It is not until then that we raise a to the power b, an
exponentiation which amounts to repeated multiplication:
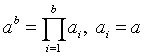
There is no reason to assume that the number of the kind of arithmetic
operations with their inverse counterparts would be exhausted now.
At least in theory we could go on reiterating forever.
If we find addition and subtraction on the zeroth level of reiteration
(for there is no systematic repetition on that level), multiplication and
division on the first level of reiteration, and exponentiation and evolution
on the second level, there must be something like reiterative exponentiation on
the third level of reiteration, even
tho** it has no name of its
own.
If we possess a general system of reiterative operations we have no need
of such names and phrases as exponentiation or the raising of a
number to a power and evolution or the extraction of a
root.
If we possess a general system of reiterative operations we can use
substantive, systematic names to give a place to these operations, whether
or not they (already) exist in common mathematical discourse.
THE BASICS OF A UNIVERSAL SYSTEM
From phrases such as repeated or iterative addition and
(re)iterative multiplication it may seem that these adjectives
are (also) used as synonyms.
As demonstrated above, i myself draw a conceptual distinction between
repetitions which are 'merely' coincidental and repetitions which are
systematic and i will use (re)iterative and (re)iteration
only if and when the repetition is a systematic one.
What is iterative in this usage is, therefore, repeated, but what is
repeated need not be iterative.
This distinction, however, will not play a further role in the present
article.
For the system of iterative operations a notation which shows some
similarity with the use of the addition and multiplication signs and/or
the enlarged capital letter sigma for an
n-ary sum and pi for an
n-ary product is certainly to be
preferred, because of the role these symbols play or can be made to play
on the lower levels of iteration.
There are important differences with the use of sigma and pi, however.
The first one is that under these signs each
ai between a1 and
ab may differ from any other
ai, whereas all ai are
the same in an iterative operation.
This means that we do not have to indicate a range for
ai and that we do not need an index for
ai.
All we need is a and the number of times it will be repeated, which
is b in the examples used so far.
The second important difference is that the sigma and pi symbols are
linked to a specific binary operation, whereas the new repetition symbol
which applies to a collection of arithmetic operations, starting with the
zeroth level of iteration and continuing with the first, second and
higher levels of iteration, will pertain to a ternary operation.
For besides the arguments a and b there is also an argument
indicating the level of iteration.
Just as the plus and times signs are put between a
and b, so i will put the universal iteration symbol between
a on the left and b on the right.
The number indicating the level of iteration can, then, be put at the top
of it, at the place where we find the last index number (the end of a
range) under sigma and pi.
Anyone really interested in a good symbol for systematic repetition should
not turn to a language (classical or not) with a script of letters which
have no meaning by themselves whatsoever, but to a language which uses a
syllabic script of characters in which each character normally represents
one particular morpheme.
The most widely used morphosyllabic script in the world provides precisely
what we need: the character 重 for again
with the fundamental meaning of to repeat or repetition, if
pronounced "chong" (instead of "zhong", which means weight,
heavy or important).
It has the decimal Unicode 37325 and the hexadecimal Unicode 91CD.
(Combining 千, "qian" meaning thousand, and 里, "li"
meaning mile, 重 has no fewer than nine strokes.
I must admit that i therefore tend to abbreviate this 'thousand-mile'
character to the three-stroke 工, pronounced "gong", in fast informal
writing.
This simple gong character depicts an ancient carpenter's square
from which the meaning of work was derived.)
We are now able to describe an arithmetic operation on the l-th
level of iteration in universal terms as follows:

CHONG SYMBOL, WITH EXPRESSION IN WORDS (AND IN
INFORMAL HANDWRITING)
In this notation i will call a "the object (number)",
l "the level (number)" and b "the counter".
The use of a preposition before the counter, and not before the object
number emphasizes that, in general, a and b cannot be
interchanged without yielding a different result.
The preposition is the one commonly used with to multiply.
Because of practical constraints i will not be able to use the above
notation (in display mode) as an integral part of a text.
When staying inline i will have to write
"a重lb".
In this typographical variant the level number appears as a superscript at
the top right of the chong symbol.
(As the superscript accompanies a symbol which stands for an operator, it
cannot be confused with a superscript accompanying a base number and
representing a power.)
Addition is a 'chong-0 operation', multiplication a 'chong-1 operation',
and exponentiation a 'chong-2 operation' as demonstrated in the following
three equations:
These equations need, of course, a formal definition of
重l, to say the least, but before
embarking upon this, i would like to show how an operation on the second
level can be expressed in one on the first level, and an operation on the
first level in one on the zeroth level of iteration.
To start with: a重1b =
(...((a1+a2)+a3) ...
+ ab-1)+ab in which
ai=a.
Since ai+ai+1 =
ai重0ai+1,
a重1b =
((...((a1重0a2)重0a3) ...
)重0ab-1)重0ab.
Similarly,
a重2b =
(...((a1·a2)·a3) ...
· ab-1)·ab in which
ai=a.
Since ai·ai+1 =
ai重1ai+1,
a重2b =
((...((a1重1a2)重1a3) ...
)重1ab-1)重1ab.
A MATHEMATICAL SEQUENCE OF OPERATORS
Each value of l in 重l defines
an individual operator.
For a formal definition of 重l i will
treat these individual operators as members of a sequence.
Each member after the first one will be defined in terms of the previous
member, while the first member is defined separately.
In this sequence the first member is the one with l=0.
For the following members, with l≥1 i will universalize the
regularities in the transition from the chong-0 to the chong-1 and from the
chong-1 to the chong-2 operation as written out above.
The general formula for the l-th iterative operator is then:
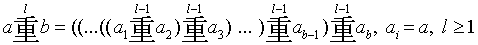
DEFINITION OF THE l-TH
ITERATIVE OR 'CHONG-l' OPERATOR
The chong-0 operator will be defined without iteration, but note that
it is entirely legitimate for b to be equal to a:
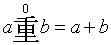
DEFINITION OF THE ZEROTH ITERATIVE
OR 'CHONG-0' OPERATOR
When we see the term 2a or 2·a in an equation we
cannot be completely sure whether this should be interpreted as
a重0a or as
a重12, even tho the outcome is the same.
Those who care about outcomes only need not mind, but should not forget
that then you might as well write something like
"1·a+a·90".
The same applies to a formula from physics such as
E=m·c2.
When using chong operators in this equation, should this be interpreted as
E=m·(c·c) then?
If so, the correct or preferred formula is
E=(c重1c)重1m.
If not, the formula may be
E=(c重22)重1m.
Taking the highest level of iteration as criterion, i shall call the
former formula "a first-level" or "chong-1 formula", the latter a
"second-level" or "chong-2 formula".
Just like subtraction is the inverse of addition, division the inverse of
multiplication and evolution the inverse of exponentiation, so all other chong
operators and operations have their inverses too.
The level number of an inverse operator is the exact opposite of the
level number of the operation inverted.
Not only will +1, +2, +3, et cetera become -1, -2, -3, but also +0 will
become -0.
There is, of course, no difference between +0 and -0 in arithmetic, and
there is no need to make such a difference in a chong calculus either, but
for the index of the operator we will have to make it, because
addition and subtraction are both operations on the zeroth level of
iteration.
The index +0 stands for addition, -0 for subtraction; +1 for
multiplication, -1 for division, and so on.
When no confusion is possible, the + sign may be deleted, as in the case of
ordinary counting.
The idea behind the formal definition for the inverse chong operation is no
different from what underlies the definition g( (x))=x,
in which g is the inverse function which undoes the invertible function
:
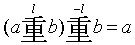
DEFINITION FOR THE INVERSE CHONG OPERATORS
The general picture of equations for both the 'chong-plus' and the inverse
'chong-minus' operators on the first three levels of iteration is now:
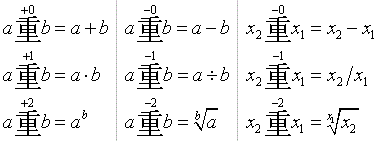
The first column shows equations which have been given before above, but
now with clear plus signs in the level numbers (even for 0).
The second column shows the inverses with clear minus signs (even for 0)
and the usual letters a and b for the object number and the
counter.
The third column is, strictly speaking, superfluous.
Only the variable x2 is used instead of a and
x1 instead of b.
However, x1 and x2 are the usual
representations for the first and second members of sequences.
The value x2-x1 is what is
traditionally called "the common difference of an arithmetic sequence",
such as 2, 4, 6, 8, ..., where x2-x1=2,
the addend of the sequence.
The value x2/x1 is what is
traditionally called "the common ratio of a geometric sequence", such as
2, 4, 8, 16, ..., where x2/x1=2, the
factor of the sequence .
And the value x1√x2
plays the same role in a sequence such as 2, 4, 16, 256, ..., where
x1√x2=2, the power
of the sequence.
It looks very attractive to have one formula for one of the main values
which characterizes a sequence, only dependent on the level of iteration
+l it belongs to:
x2重-lx1.
But the use of this formula would suggest that
x2重-lx1 =
xk+1重-lxk
for any k, and not just for k=1; otherwise the value would
not be typical of the whole sequence at all.
The above example of a second-level sequence proves already that this
is not the case in general, for whereas 2√4=2,
16√256=16√28=√2, which
is not the power used in 162=256.
We will return to this issue and see what are the correct formulas when
discussing chong-0, chong-1, chong-2 and higher-level number sequences.
THE CHONG TABLES AND THEIR SEQUENCES
We all are like small children on the higher levels of iteration, but on
the lower levels —on the first level to be precise— adults
should know their multiplication tables.
If not, i will repeat the one- to four-times tables in a common display,
but only for the first four results.
I will even offer an addition table, but again only for
1≤a≤4 and 1≤b≤4.
After that we are going to have a look at an exponentiation table with the same
arguments, and still with numbers which are peanuts to those which will be
produced later.
It is not until the fourth iteration table of chong-3 operations that we
will face the difficulty of numbers which we can hardly write down anymore
(in chong-2 notation).
As (re)iteration is a term quite generally used in mathematics, i will
more specifically call these tables "chong tables": "the chong-0 table",
"the chong-1 table", "the chong-2 table", and so on.
The three lower-level chong tables may be little exciting in the eyes of
those interested in results only, but for each row of figures i have added
the name of the sequence involved, which should bring the figures to life.
These names are based on the terminology introduced in my paper
A substantive terminology for sequences and
cycles.
In that paper i have drawn a sharp distinction between a definition and a
calculation formula, which, with one exception, operate on different
levels: multiplication (but also addition) in the calculation formula
corresponds with addition in the definition formula, exponentiation in the
calculation formula with multiplication in the definition formula.
In a definition formula of a sequence each member
xn, with the exception of the first one, is expressed
in terms of one or more previous ones (xn-1,
xn-2, ...).
As stated above the general formula for the l-th iterative
operator is
a重lb =
((...((a1重l-1a2)
重l-1a3) ...
)重l-1ab-1)重l-1ab.
From this formula it follows that
a重l(b-1) =
(...((a1重l-1a2)
重l-1a3) ...
)重l-1ab-1.
Hence, for every l≥1
a重lb =
(a重lb-1)
重l-1a.
In the sequence which accompanies the operation in a chong-l table
for which l≥1 a member xb of the
sequence has the value
a重lb, while
xb-1 =
a重l(b-1).
Therefore, for each value of a the value of the b-th member
in the sequence is:
xb = (xb-1)重l-1a
This means that for a chong-l table (l≥1), the definition
formula of the sequences is a chong-(l-1) formula, and for each
sequence we can obtain a new member of the sequence by performing a
chong-(l-1) operation on the previous member.
If we do not start from the chong-l operation, but from a
chong-l sequence, then the general definition formula for
that sequence is
xn+1 = xn重la,
where l≥1.
It is this general formula which underlies the definition of a
functor f for any l, inclusive of +0 and -0:
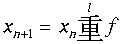
DEFINITION FOR A SEQUENCE FUNCTOR
(In the context of the chong operations the term functor is used as
the universal term for what is an addend in addition, a subtrahend in
subtraction, a factor in multiplication, a divisor in division, a power in
exponentiation and a root in evolution on the lower levels of iteration.)
It follows that
x2 = x1重lf.
At the same time, according to the definition of an inverse chong operator,
(x1重lf)重-lf=x1.
Hence,
x2重-lf=x1.
And here we see the mistake in believing that
x2重-lx1
would be a characteristic value of the whole sequence, such as the addend
('common difference') or factor ('common ratio'), for only if and when
f=x1 is
x2重-lf
the same as
x2重-lx1!
Nonetheless, except for the chong-0 table, we will see that this is indeed
the case for the sequences in the chong tables i am going to discuss.
The first three of these tables are:

|
CHONG (PLUS) 0 |
|
PLUS-ZEROTH LEVEL OF ITERATION
ADDITION |
|
b=1 |
|
2 |
|
3 |
|
4 |
|
SEQUENCE |
| a=1 |
2 |
|
3 |
|
4 |
|
5 |
|
head-2 addend-1 (addition) sequence |
| 2 |
3 |
|
4 |
|
5 |
|
6 |
|
head-3 addend-1 (addition) sequence |
| 3 |
4 |
|
5 |
|
6 |
|
7 |
|
head-4 addend-1 (addition) sequence |
| 4 |
5 |
|
6 |
|
7 |
|
8 |
|
head-5 addend-1 (addition) sequence |

|
CHONG (PLUS) 1 |
|
PLUS-FIRST LEVEL OF ITERATION
MULTIPLICATION |
|
b=1 |
|
2 |
|
3 |
|
4 |
|
SEQUENCE |
| a=1 |
1 |
|
2 |
|
3 |
|
4 |
|
head-1 addend-1 (addition) sequence |
| 2 |
2 |
|
4 |
|
6 |
|
8 |
|
head-2 addend-2 (addition) sequence |
| 3 |
3 |
|
6 |
|
9 |
|
12 |
|
head-3 addend-3 (addition) sequence |
| 4 |
4 |
|
8 |
|
12 |
|
16 |
|
head-4 addend-4 (addition) sequence |

|
CHONG (PLUS) 2 |
|
PLUS-SECOND LEVEL OF ITERATION
EXPONENTIATION |
|
b=1 |
|
2 |
|
3 |
|
4 |
|
SEQUENCE |
| a=1 |
1 |
|
1 |
|
1 |
|
1 |
|
head-1 factor-1 (multiplication) sequence |
| 2 |
2 |
|
4 |
|
8 |
|
16 |
|
head-2 factor-2 (multiplication) sequence |
| 3 |
3 |
|
9 |
|
27 |
|
81 |
|
head-3 factor-3 (multiplication) sequence |
| 4 |
4 |
|
16 |
|
64 |
|
256 |
|
head-4 factor-4 (multiplication) sequence |
The definition formula for the sequences in the chong-0 table cannot be
based on the formula
xb = (xb-1)重l-1a.
It is simply based on the counter's acting as an addend here and the
progression of b as a natural number:
xb=(xb-1)+1.
The addition sequences start with a+1 in the column for which
b=1.
Their specific names are therefore head-a+1 addend-1 addition
sequence.
The definition formula for the sequences in the chong-1 table
is xb=(xb-1)+a,
because
(xb-1)重0a =
(xb-1)+a.
Both the heads and the addends in these sequences vary as a varies.
Their specific names are therefore head-a addend-a
addition sequence.
In the universal names we will not make use of traditional terms like
addition and addend.
For the sequences in the chong-0 and chong-1 tables these names are:
head-1, -2, -3,
-4 or -5 functor-1,
-2, -3 or -4
chong-0 sequence.
On the second level of iteration
(xb-1)重l-1a =
(xb-1)重1a.
Hence, the definition formula for the sequences in the chong-2 table is
xb=(xb-1)·a.
Again, the table shows their specific names, this time referring to a
multiplication (a chong-1 operation) and a factor (a chong-1 functor).
Their universal names are, apart from the head element:
functor-1, -2, -3
or -4 chong-1 sequence.
We have now arrived at the third level of iteration, the level of
iterative exponentiation.
It is still possible to express the chong operation on this level in
traditional notation:
Just as a multiplication is reduced to an addition in
am·al =
am+l, so an exponentiation (one of two) is
reduced to a multiplication in
(am)l =
am·l.
It follows from this equation that
a重3b =
aa2·a3...·ab,
where ai=a.
In this way the chong-3 operation is reduced to a chong-2 operation in the
calculation.
The exponent is now a multiplied b-1 times by itself.
Conversely,
aa2·a3...·ab =
(aa2·a3...·ab-1)ab.
Hence, for every increase of b by 1 unit, the result is raised to
the power ab, which is equal to a.
This is in agreement with our general formula
xb = (xb-1)重l-1a
and explains why all sequences formed in the following table are
head-a power-a exponentiation sequences:

|
CHONG (PLUS) 3 |
|
PLUS-THIRD LEVEL OF ITERATION
ITERATIVE EXPONENTIATION |
|
b=1 |
|
2 |
|
3 |
|
4 |
|
SEQUENCE |
| a=1 |
1 |
|
1 |
|
1 |
|
1 |
|
head-1 power-1 (exponentiation) sequence |
| 2 |
2 |
|
4 |
|
16 |
|
256 |
|
head-2 power-2 (exponentiation) sequence |
| 3 |
3 |
|
27 |
|
19683 |
|
327 |
|
head-3 power-3 (exponentiation) sequence |
| 4 |
4 |
|
256 |
|
416 |
|
464 |
|
head-4 power-4 (exponentiation) sequence |
|
Note: 3重34=327.
In standard notation this number is too large for the table, but it
is in full: 7,625,597,484,987.
4重33=416.
416=(22)16=232.
This number is in full: 4,294,967,296.
4重34=464.
464=(22)64=2128.
This number is in full:
340282366920938463463374607431768211456.
|
Since on this level of iteration
(xb-1)重l-1a =
(xb-1)重2a,
the definition formula for the sequences in this chong-3 table
is xb=(xb-1)a.
The specific names in the table refer to exponentiation and a power of 1, 2, 3
or 4.
However, universal names only refer to the chong level and the value of the
functor at that level.
They are, apart from the head element:
functor-1, -2, -3
or -4 chong-2 sequence.
Some of my readers may want to pull out now, because they find the value
of 4重34, a number of 39 digits
long, already 'astronomical'.
Anyone may, of course, pull out at any time, but i hope not for the wrong
reason.
The numbers growing too large in these tables is not a reason for
quitting, for —if necessary, i will repeat this ad nauseam—
numbers are not (too) large in any absolute sense, they may only be large
in a certain context and too large for a certain numeral system.
So, we will continue our tour de force.
For the fifth iteration table, the chong-4 table, we will have to swim
into the sea of numbers without the help of a raft inscribed with the
handy formulas of traditional arithmetic and besprinkled with the letters
of Mediterranean antiquity.
But being thrown upon our own resources will only give us a better
sense of direction.
We should have done it before: return to the formal definition of the
chong operators.
The chong-4 operator is, then, the variant of the universal formula for
which l=4.
In other words:
a重4b =
((...((a1重3a2)
重3a3) ... ) 重3ab-1)
重3
ab
With this specific formula we are able to do all calculations from
1重41 to
4重44, which we have confined
ourselves to.
I will leave it to the reader to calculate or check the values of
1重41 to 1重44,
2重41 to 2重43,
3重41 to 3重42
and 4重41 to 4重42,
with or without consulting the above chong-3 table.
The calculation of the other values could require some further explanation,
i believe.
I will start with 2 chong-4 by 4.
2重44 =
((a1重3a2)
重3a3)
重3a4, in which
ai=a=2.
Hence, 2重44 =
((2重32)
重32)
重32 =
(4重32)
重32, in which
4重32=256
(see the chong-3 table).
Hence, 2重44 =
256重32=256256.
Next i will consider 3 chong-4 by 3 and by 4.
3重43 =
(a1重3a2)
重3a3, in which
ai=a=3.
Hence,
3重43 =
(3重33)
重33, in which
3重33=19683 (see the chong-3 table).
Hence,
3重43 =
19683重33 =
1968319683·19683=19683387420489.
As 3重44 =
(3重43)重33,
3重44 =
(19683387420489)重33 =
(19683387420489)((19683^387420489)·(19683^387420489)) =
(19683387420489)(19683^(387420489+387420489)) =
(19683387420489)(19683^774840978) =
19683(387420489·19683^774840978) =
19683((19683^2)·(19683^774840978)) =
19683(19683^774840980).
(I resort to a ^ sign for exponentiation where the font for the exponent
would otherwise become too small.)
Let us complete the chong-4 table with 4 chong-4 by 3 and by 4.
4重43 =
(4重34)
重34, in which
4重34=464 (see the
chong-3 table).
Hence,
4重43 =
(464)重34 =
(464)((4^64)·(4^64)·(4^64)) =
(464)(4^(64+64+64)) =
(464)(4^192) =
4(64·(4^192)) =
4((4^3)·(4^192)) =
4(4^195).
The last value to be calculated is 4重44 =
(4重43)重34
in which 4重43 =
4(4^195).
I conclude that
4重44 =
(4(4^195))重34 =
(4(4^195))((4^(4^195))·(4^(4^195))·(4^(4^195))) =
(4(4^195))(4^(3·(4^195))) =
4((4^195)·(4^(3·(4^195)))) =
4(4^(3·(4^195)+195)).

|
CHONG (PLUS) 4 |
|
|
PLUS-FOURTH LEVEL OF ITERATION |
|
b=1 |
|
2 |
|
3 |
|
4 |
|
SEQUENCE |
| a=1 |
1 |
|
1 |
|
1 |
|
1 |
|
functor-1 chong-3 |
| 2 |
2 |
|
4 |
|
256 |
|
256256 |
|
functor-2 chong-3 |
| 3 |
3 |
|
19683 |
|
19683387420489 |
|
19683(19683774840980) |
|
functor-3 chong-3 |
| 4 |
4 |
|
464 |
|
4(4195) |
|
4(4(3·(4^195)+195)) |
|
functor-4 chong-3 |
|
Note: i will not attempt to give all numbers in full, in standard notation,
anymore.
4重42 =
4重34 = 464 =
2128, whose value can still be found under the chong-3
table above.
But even the exact value of 2重44 =
256256=(28)256 =
2(8·256) =
22048 is beyond my (modest) means.
The value of 4重43 =
4(4^195).
This equals
(22)((2^2)^195) =
(22)(2^390) =
2(2·2^390) =
2(2^391).
|
The definition formula for the sequences in this chong-4 table
is based on
xb =
(xb-1)重3a.
From the point of view of our new, universal system of operators we could
leave it at that, but i shall also provide a version which does not make
use of an operation higher than exponentiation so that the formula will be
suitable for calculating the next member of a sequence.
Given that
(xb-1)重3a =
((...(((xb-1)1重2(xb-1)2)
重2(xb-1)3) ... )
重2(xb-1)a-1)
重2(xb-1)a
the value of xb will be
((...(((xb-1)1
(xb-1)2)
(xb-1)3) ... )
(xb-1)a-1)
(xb-1)a =
(xb-1)1((xb-1)2·(xb-1)3· ...
·(xb-1)a-1·(xb-1)a) =
(xb-1)
((xb-1)^(a-1)).
(The brackets are very important here, for
(xb-1)
((xb-1)^(a-1)) is
certainly not the same as
((xb-1)
(xb-1))(a-1)!)
It follows that for a=1 the definition formula is
xb =
(xb-1)
((xb-1)^0) =
xb-1.
For a=2 it is
xb =
(xb-1)
((xb-1)^1) =
(xb-1)
(xb-1).
For a=3 it is
xb =
(xb-1)
((xb-1)^2).
And for a=4 it is
xb =
(xb-1)
((xb-1)^3).
For example, 3重42 =
3(3^2)=39=19683,
while the next element in the sequence is
19683(19683^2)=19683387420489.
On this level of iteration there are no specific, traditional names
anymore.
As in all chong tables but the first one, where the definition formula is
xb =
(xb-1)重la
or
xb =
(xb-1)重lf
also for the chong-3 functors f=a.
The four universal names of the sequences are therefore:
head-1, -2, -3 and
-4 functor-1, -2,
-3 and -4 chong-3 sequence.
When looking at the five tables presented so far three patterns keep on
returning.
First of all, for all l≥1
a重l1=a for every a
in the first column of each table.
This is because for b=1,
a重lb=a1=a.
Then, for l≥2,
1重lb=1 for
every b in the first row of each table.
This is because for a=1,
1重2b =
((...((1重11)重11) ...
重11)重11.
In this equation every
1重11=1.
Once this is fixed on the second level, it will remain so on all following
levels, because each higher-level operator is defined in terms of the
previous one.
The third pattern is less conspicuous, if only because it does not show
within one table but between two consecutive tables.
Those with a keen eye for the behavior of numbers will have noticed already
that in every chong table the numbers on the diagonal fill the second
column of the next table, that is, the column for b=2.
But this phenomenon need not surprise us either.
It can be proved to be correct in the following simple, if not trivial,
way:
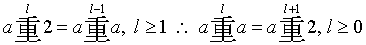
This also explains why
2重l2=4
on any level of iteration, given that
2重02=2+2=4,
altho this can also be proved in the following way:
2重l2 =
2重l-12 =
2重l-22 = ...
= 2重22 =
2重12 =
2重02 = 4.
So, out of sixteen results in the following and last 4-by-4 chong table ten
results are already known, and we only have to calculate the remaining six.
They are 2重53,
2重54,
3重53,
3重54,
4重53 and
4重54.
This time we will first develop the definition formulas of the chong-4
sequences and then calculate the remaining numbers with the higher index by
performing a chong-4 operation on the previous number using the new
formula.
In order to make it a little bit easier for myself and the reader i will
not try to develop one formula for all a's at once, as i did above.
Instead, i will develop a formula for each sequence formed by a row of
numbers separately.
As all numbers in the first row are already given, i will start with
a=2.
In this case xb =
(xb-1)重42 =
(xb-1)重3(xb-1).
We already found that
(xb-1)重3a =
(xb-1)((xb-1)^(a-1)), so
xb =
(xb-1)((xb-1)^((xb-1)-1)).
We should check this for b=2:
x2=x1((x1)^((x1)-1)) =
2(2^(2-1))=4, which is correct.
The third number of the sequence
x3=x2((x2)^((x2)-1)) =
4(4^3)=464=2128, a number we encountered
before in the chong-4 table and the chong-3 table, where it is given in
full.
The fourth member of the same chong-4 sequence is
x4=x3((x3)^((x3)-1)) =
(464)((464)^((464)-1)) =
(2128)((2128)^((2128)-1)),
a number i cannot reasonably be expected to write out in standard notation,
when even the value of the exponent by itself is beyond my present
means.
When developing the sequence formula for a=3 i will make use of
'abbreviations' which should make it easier to read the intermediate
equations.
The first such abbreviation will only save us a subscript of three
characters and occasionally some extra brackets:
t=xb-1.
Now
xb=t重43 =
(t重3t)重3t =
(t(t^(t-1)))重3t.
Here i introduce a second abbreviation: T=t(t^(t-1)).
Now
xb=T重3t =
((...((T1重2T2)
重2T3) ... )
重2Tt-1)
重2Tt =
((...((T1T2)
T3)...)Tt-1)
Tt =
T1(T2·T3·...·Tt-1·Tt) =
T(T^(t-1)).
At this point i will substitute t(t^(t-1))
for T again.
(Note the great but not complete analogy between
T(T^(t-1)) and
t(t^(t-1)).)
So
xb=(t(t^(t-1)))((t^(t^(t-1)))(t-1)) =
(t(t^(t-1)))(t^((t-1)·(t^(t-1)))) =
t((t^(t-1))·(t^((t-1)·(t^(t-1))))) =
t(t^((t-1)+(t-1)·(t^(t-1)))) =
t(t^((t-1)·((t^(t-1))+1))).
Substituting xb-1 for t, the definition
formula for the chong-4 sequence with 3 as object turns out to be:
xb = xb-1(xb-1((xb-1-1)·((xb-1(xb-1-1))+1)))
Just like above, we will check this result first for b=2.
For this value
x2 = x1(x1^((x1-1)·((x1^(x1-1))+1))).
Since x1=3,
x2 = 3(3^((3-1)·((3^(3-1))+1))) =
3(3^(2·((3^2))+1)))=3(3^20).
We know from the chong-4 table that
3重43=19683387420489=3重52.
The chong-4 value was calculated on the basis of
3重43 =
(27^3)((27^3)·(27^3)) =
((3^3)^3)(((3^3)^3)·((3^3)^3)) =
(3^3)(3·((3^3)^6)) =
(3^3)(3^19)=3(3·(3^19))=3(3^20),
which is indeed the same value for x2.
For b=3 the value of
xb-1 =
3重52 =
19683387420489 =3(3^20).
Hence,
xb=[3{3^20}]{[3^{3^20}]^{([3^{3^20}]-1)·(([3^{3^20}]^([3^{3^20}]-1))+1)}} =
3{(3^20)·([3^{3^20}]^{([3^{3^20}]-1)·(([3^{3^20}]^([3^{3^20}]-1))+1)})} =
3{(3^20)·(3^{(3^20)·([3^{3^20}]-1)·(([3^{3^20}]^([3^{3^20}]-1))+1)})} =
3{(3^{(3^20)·([3^{3^20}]-1)·(([3^{3^20}]^([3^{3^20}]-1))+1)})+20} =
3{(3^{3486784401·([19683387420489]-1)·(([19683387420489]^([19683387420489]-1))+1)})+20}.
The outcomes for
3重54,
4重53 and
4重54 will only be more
complicated than the one above for
3重53.
So, i will call it "a table" (rather than "day") and leave the three
remaining operations with question marks:

|
CHONG (PLUS) 5 |
|
|
PLUS-FIFTH LEVEL OF ITERATION |
|
b=1 |
|
2 |
|
3 |
|
4 |
|
SEQUENCE |
| a=1 |
1 |
|
1 |
|
1 |
|
1 |
|
functor-1 chong-4 |
| 2 |
2 |
|
4 |
|
464 |
|
(464)((464)^((464)-1)) |
|
functor-2 chong-4 |
| 3 |
3 |
|
19683387420489 |
|
[SEE NOTE] |
|
? |
|
functor-3 chong-4 |
| 4 |
4 |
|
4(4(3·(4^195)+195)) |
|
? |
|
? |
|
functor-4 chong-4 |
|
Note: the value of 3重53 is
3((3^(3486784401·((19683387420489)-1)·(((19683387420489)^((19683387420489)-1))+1)))+20).
|
A HIGHER-LEVEL NOTATION FOR NUMBERS?
The algebraic equation
a0·xn +
a1·xn-1 + ... +
an-2·x2 +
an-1·x +
an = 0, where
a0, a1, ... are integers (not all zero),
is definitely a second-level formula in which exponentiation plays an essential
role, not because it must take place, but because the formula does not
allow for any higher-level operation.
Numbers which satisfy such an equation are called "algebraic numbers" (as
distinct from "transcendental numbers").
We find the equation back in the formula for nonnegative integers in the
standard multi-place place-value system with a base number b:
w = a0·bn +
a1·bn-1+...+
an-3·b3 +
an-2·b2 +
an-1·b + an
0≤ai<b
Let us transform this notational formula step by step without changing the
place of any ai as far as their order is concerned:
w = (((...((a0·bn) +
(a1·bn-1)) + ... +
(an-3·b3)) +
(an-2·b2)) +
(an-1·b)) +
an
w = (((...((a0·(b重2n)) +
(a1·(b重2n-1))) + ... +
(an-3·(b重23)))
+
(an-2·(b重22))) +
(an-1·(b重21))) +
(an·(b重20))
w = (((...((a0重1(b重2n)) +
(a1重1(b重2n-1))) + ... +
(an-3重1(b重23)))
+
(an-2重1(b重22))) +
(an-1重1(b重21))) +
(an重1(b重20))
w = (((...((a0重1(b重2n))
重0
(a1重1(b重2n-1)))
重0 ...
重0
(an-3重1(b重23)))
重0
(an-2重1(b重22)))
重0
(an-1重1(b重21)))
重0
(an重1(b重20))
In this formula the three lower-level iterative operators occur and
reoccur from right to left in descending order, except for one
重0 missing at the very beginning.
But the formula could also have started with, for instance,
a-1重0 and a-1=0,
for a zero in front of a number does not change its value.
The reason why i discuss this formula, however, is not only that it is a
nice example of three chong operators in a row, and even being repeated
together that way, which is more a question of form than of content.
No, i also have a substantive reason: the standard multiplace place-value
notation for numbers is a chong-2 notation!
Such a notation may work and suffice for formulas which are of the second
and lower levels of iteration themselves, but why should it still be
satisfactory on (much) higher levels of iteration?
On the higher levels the numbers will run amok in a chong-2 notation,
for base 10 and even more so for lower base numbers.
They may be too big for a chong-2 system, numbers are never (too) big or
(too) small by themselves, with the exception, perhaps, of the number 1
among natural numbers.
The universalization of traditional mathematical operations by means of a
chong operator which can be defined and made to work on any level of
iteration is of fundamental significance and interesting enough, but it
evokes the question whether it can and will ever be of practical use when
we keep on writing down numbers in a notation which does not transcend
exponentiation on the chong-plus-2 level.
As a chong-plus-3 or higher-level notation for numbers is beyond the scope
of the present paper, i invite the reader to puzzle out what a chong-3
notation for numbers, if at all possible, will look like.
(Something like the above formula for the chong-2 notation, but now with
four consecutive chong operators, you would say.)
67.CEN
| * |
The first-person singular pronoun is
spelled with a small i, as i do not consider myself a Supreme
Being or anything else of that Ilk. |
| ** |
Where there is some existing orthographical
variation preference will be given to the (more) phonematic
variant |
|